
Algebraic long division is very similar to traditional long division (which you may have come across earlier in your education).
Example:
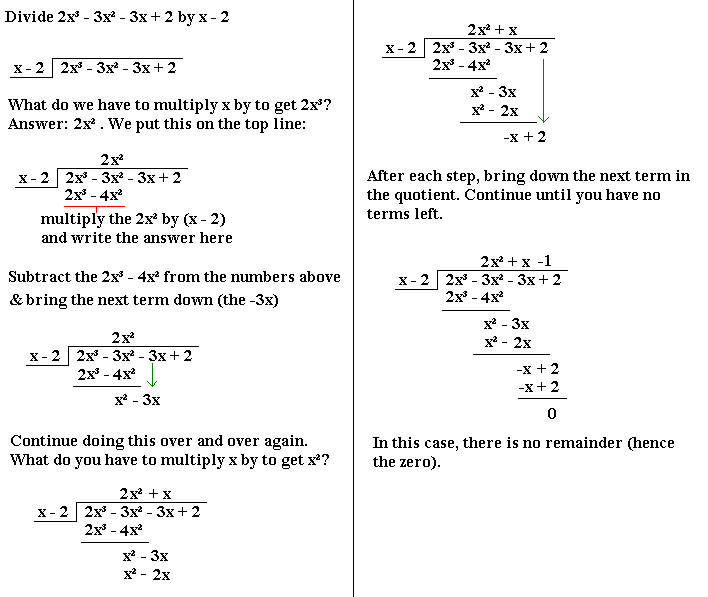
NB:
If the quotient (the polynomial that you are dividing) has a term in x missing, add such a term by placing a zero in front of it. For example, if you are dividing x³ + x - 4 by something, rewrite it as x³ + 0x² + x - 4 .
For algebraic long division practise makes perfect- the best way to learn how to do them properly is to do loads of examples until you get them right every time!
The Remainder Theorem
When dividing one algebraic expression by another, more often than not there will be a remainder. It is often useful to know what this remainder is and it can be calculated without going through the process of dividing as above. The rule is:
If a polynomial f(x) is divided by ax - b, the remainder is f(b/a)
In the above example, 2x³ - 3x² - 3x + 2 was divided by x - 2.
Let f(x) = 2x³ - 3x² - 3x + 2 , a = 1, b = 2. The remainder is therefore f(2) = 2×2³ - 3×2² - 3×2 + 2 = 0, as we saw when we divided the whole thing out.
The Factor Theorem
This states:
If x - a is a factor of the polynomial f(x), then f(a) = 0
In the above worked example, f(2) = 0. This means that (x - 2) is a factor of the equation.